4. und 5. Proton auf der 2. und 3. Schale
Wenn wir nun versuchen, die nächste Ebene mit einem Proton und einem
Neutron zu belegen, existiert keine eigene Ebene.
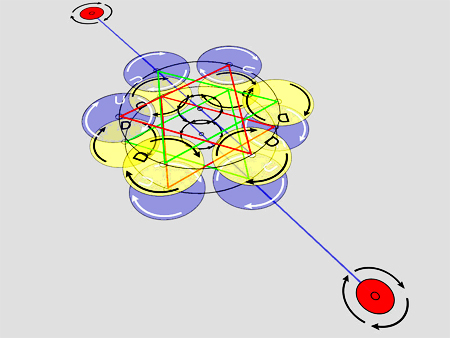
Dreht man es um 90°, wird eine Ebene doppelt besetzt.
Bild 13: Doppelt belegte Ebene
Diese Stellung führt zu einer außergewöhnlichen Instabilität der nächsten Reihe
bis zum Edelgas Neon. Das ist damit zu erklären, dass es sich bei den Quarks
in ihrer Drehrichtung und Bewegung um Ladungen handelt.
Diese würden sich gerne abstoßen. Da sie es bis dahin nicht können,
entsteht diese Instabilität.
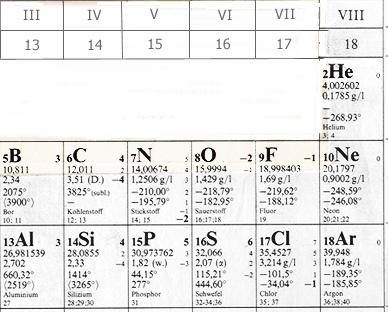
Alle Elemente über dem Kohlenstoff bis zum Neon sind leichte Gase.
Die Schmelztemperatur sinkt vom Kohlenstoff bei 3825° Celsius
auf -210° Celsius beim Stickstoff.
Tabelle 1: Periodensystem der Elemente
Diese gleiche Grundstruktur gilt auch für die Elemente der dritten Schale.
Wir haben im Silizium wieder ein Element mit hohem Schmelzpunkt (3265°)
und danach folgt Phosphor (44.5°) mit geringem Schmelzpunkt.
Er ist jedoch bei normalen Temperaturen kein Gas.
Betrachtet man den Stickstoff, so ist bei ihm eine Ebene doppelt belegt
und dabei sind die 3 Up- und 3 Down-Quarks einer jeden Ebene um 180° versetzt.
Damit hat man auf einer Ebene zwei Elektronen. Beim Neon hätten alle vier Ebenen
eine doppelte Besetzung und damit auch 2 Elektronen auf jeder dieser Ebenen.
Diese Stellung des Edelgases würde ich mit zweifach belegter
Doppelkreuzstellung bezeichnen.
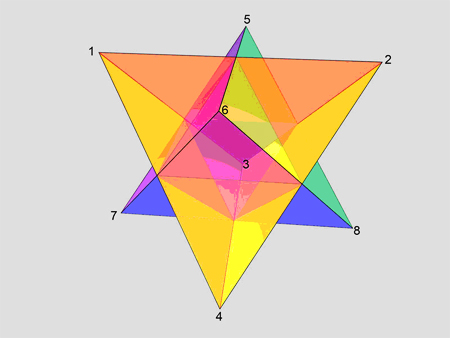
Betrachtet man nun die Elektronen in ihren Grenzstellungen, so befinden sich
vier Elektronen als Kreuz oben und vier Elektronen als Kreuz unten.
Das wären zwei ineinander gestellte Tetraeder.
Bild 14: Doppelter Tetraeder als Bild für die äußere Position
von 8 Elektronen einer Schale
Drehen sich die Elektronen aus dieser Stellung um 90°, so bewegen sich
alle genau auf der Grundebene. Hier ergibt sich ein Problem, denn zwei Elektronen
dürfen nach dem Ausschließungsprinzip nicht an einem Punkt sein. In diesem Fall
wären sogar alle vier an einem Punkt. Die Lösung liegt darin, dass Elektronen
auch nur aufgerollte zweidimensionale Wellen sind.
Da sie unterschiedliche Ebenen vorweisen, stören sie sich nicht.